复习常见的机器学习算法,并加以巩固。
Learning Algorithm
机器学习的学习算法主要分为两类监督学习和无监督学习。

Supervised Learning
Linear Regression
Cost
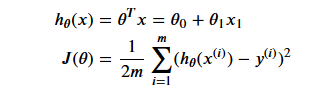
1 | def cost(Theta, X, Y): |
Gradient Descent
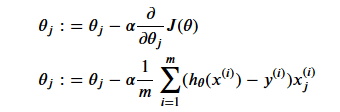
1 | def gradient(Theta, X, Y): |
Logistic Regression
Cost
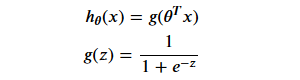
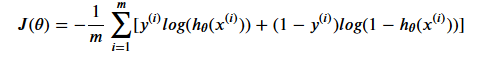
1 | def sigmoid(z): |
1 | def cost(Theta, X, Y): |
Gradient Descent
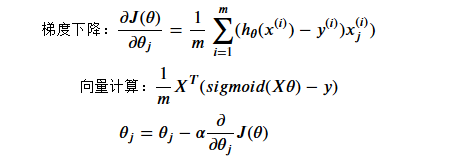
1 | def gradient(Theta, X, Y): |
Feature Mapping

1 | def feature_mapping(x, y, power, as_ndarray=False): |
Regularized Cost
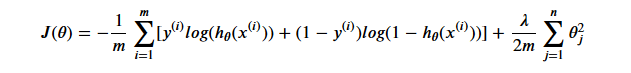
1 | def cost(Theta, X, Y, l=1): |
Regularized Gradient
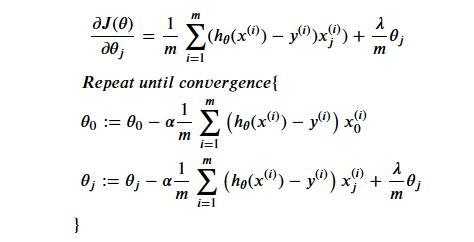
1 | def gradient(Theta, X, Y, l=1): |
Neural Network
Feed_Forward
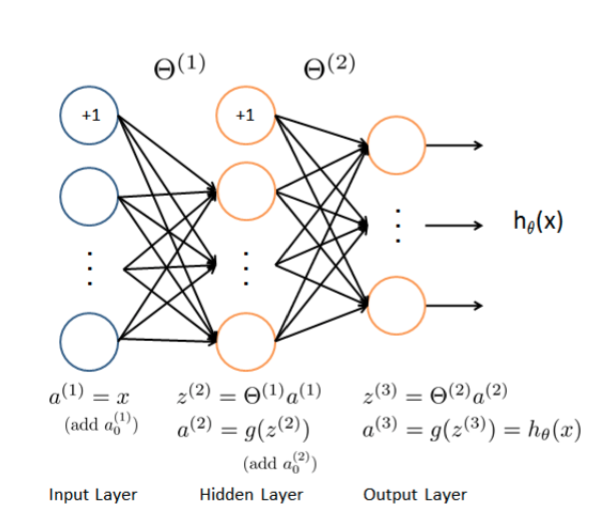
1 | def feed_forward(Thetas, X): |
Cost

1 | def cost(Thetas, X, Y): |
Regularized Cost
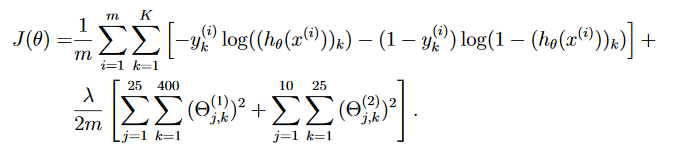
1 | def cost(Thetas, X, Y, l=1): |
Back Propagation
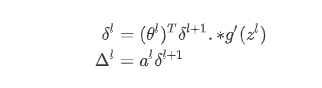
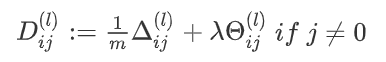
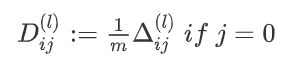
1 | def sigmoid_gradient(z): |
1 | def back_propagation(Thetas, X, Y, l): |
SVM
Gaussian Kernel
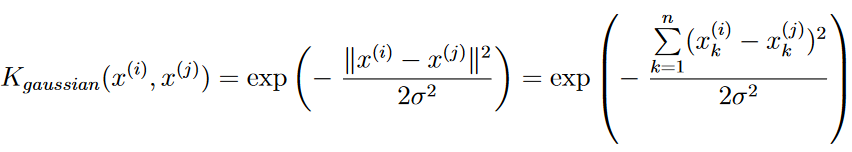

gamma和sigma成反比,gamma越小即sigma越大,gaussian kernek越”胖”,模型越容易under fitting
1 | def gaussian_kernel(X, Y, sigma): |
Unsupervised Learning
K-means
1 | def K_means(X, K): |
1 | def random_initialization(X, K): |
1 | def find_closet_centroids(X, centroids): |
1 | def compute_centroids(X, idx): |
1 | def cost(X, idx, centroids): |
PCA
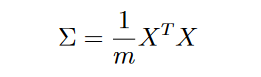
1 | def pca(X): |
1 | def project_data(X, U, K): |
1 | def reconstruct_data(Z, U, K): |
Anomaly Detection

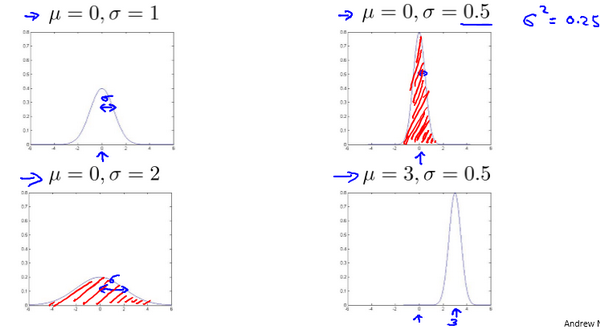
1 | def gaussian_distribution(X): |
Recommender System
Regularized Cost

1 | def cost(params, Y, R, nm, nu, nf, l=0.0): |
Regularized Gradient
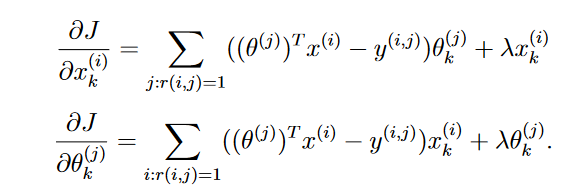
1 | def gradient(params, Y, R, nm, nu, nf, l=0.0): |
Trick
feature scaling
1 | def feature_scaling(X): |
num2vec
1 | def num2vec(y): |
serialize
1 | def serialize(Thetas): |
Gradient Check
1 | def gradient_check(Theta, X, Y, l, e= 10 ** -4): |
Error Analysis

1 | def error_analysis(yp, yt): |